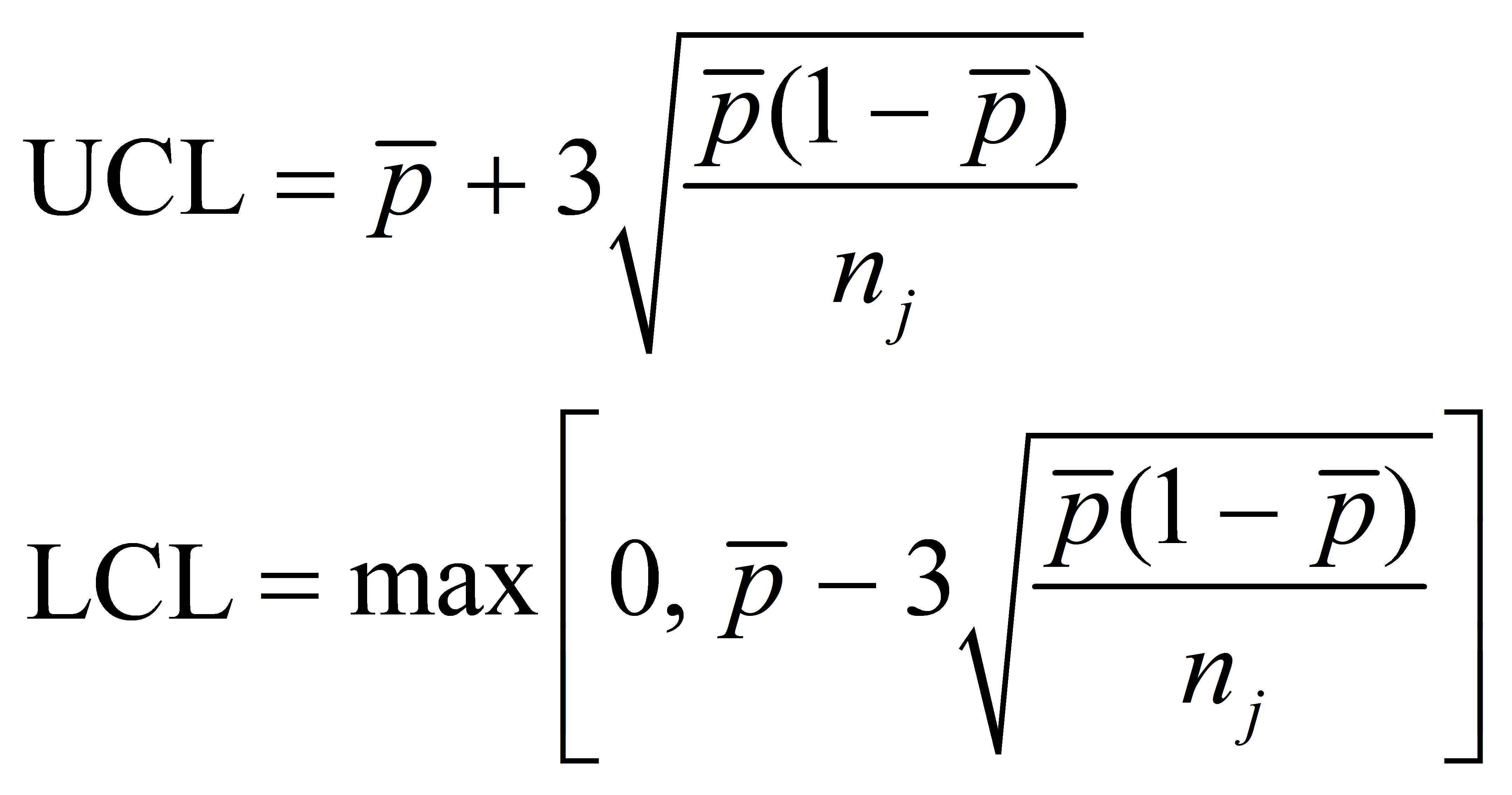Impossible? I Chart's Negative LCL Explained

Impossible? I Chart's Negative LCL Explained: A Critical Examination

Thesis Statement

Theoretical Considerations

The Negative LCL is calculated using the formula μ - 3σ, where μ is the process mean and σ is the process standard deviation. It is based on the assumption that a normally distributed process with a finite number of samples will produce a certain percentage of data points that fall below the Negative LCL, typically set at 0.135%. Proponents of the Negative LCL argue that it provides a conservative estimate of the lower limit of a process, ensuring a low probability of false alarms. However, critics question the validity of this assumption, arguing that it may not always hold true for real-world processes with non-normal distributions or skewed data.

Empirical Evidence and Practical Applications

Studies have shown that the Negative LCL can be effective in detecting process shifts in certain scenarios. In industries such as manufacturing and healthcare, where tight quality control is crucial, the Negative LCL has been used to identify deviations from target specifications. However, its effectiveness can vary depending on the underlying process characteristics, sample size, and frequency of data collection. For instance, a small sample size may result in a wider confidence interval, making it more challenging to detect small process shifts.

Despite its potential benefits, the use of the Negative LCL has also raised concerns. False alarms can lead to unnecessary process interventions and increased production costs. In high-risk industries such as pharmaceuticals or nuclear energy, where false alarms could have dire consequences, the Negative LCL may not be an appropriate control limit. Additionally, its conservative nature can result in missed opportunities for improvement, as processes may be falsely deemed stable when they are actually drifting towards an unacceptable state.

Contrasting Perspectives

Implications for Decision-Making

The decision to adopt the Negative LCL in a given situation requires a careful assessment of the potential benefits and risks. Factors to consider include the nature of the process, the sample size, the frequency of data collection, and the severity of potential consequences of false alarms. In industries with stringent quality requirements and low tolerance for deviations, the Negative LCL may be considered a necessary precaution. However, in more flexible settings where the cost of false alarms is high, alternative control limits or statistical methods may be preferred.

Conclusion

The Negative LCL of Impossible? I Chart presents a complex and controversial concept in statistical process control. While it has the potential to provide a conservative estimate of the lower process limit and detect process shifts, it also has limitations and can lead to false alarms. The validity and practical implications of the Negative LCL depend on a variety of factors, including the process characteristics, data quality, and decision-making context.